Conclude Ordered Field मुफ़्त में
Drop document here to upload
Up to 100 MB for PDF and up to 25 MB for DOC, DOCX, RTF, PPT, PPTX, JPEG, PNG, JFIF, XLS, XLSX or TXT
Note: Integration described on this webpage may temporarily not be available.
0
Forms filled
0
Forms signed
0
Forms sent
Discover the simplicity of processing PDFs online

Upload your document in seconds

Fill out, edit, or eSign your PDF hassle-free

Download, export, or share your edited file instantly
Top-rated PDF software recognized for its ease of use, powerful features, and impeccable support






Every PDF tool you need to get documents done paper-free
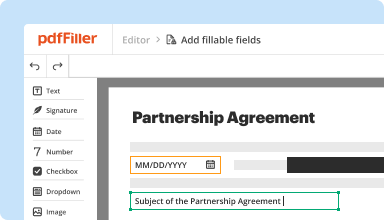
Create & edit PDFs
Generate new PDFs from scratch or transform existing documents into reusable templates. Type anywhere on a PDF, rewrite original PDF content, insert images or graphics, redact sensitive details, and highlight important information using an intuitive online editor.
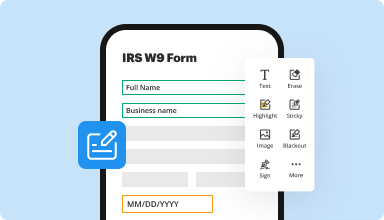
Fill out & sign PDF forms
Say goodbye to error-prone manual hassles. Complete any PDF document electronically – even while on the go. Pre-fill multiple PDFs simultaneously or extract responses from completed forms with ease.
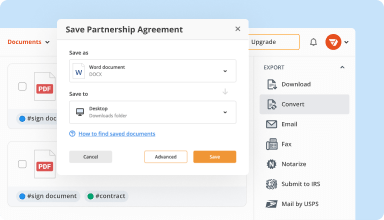
Organize & convert PDFs
Add, remove, or rearrange pages inside your PDFs in seconds. Create new documents by merging or splitting PDFs. Instantly convert edited files to various formats when you download or export them.
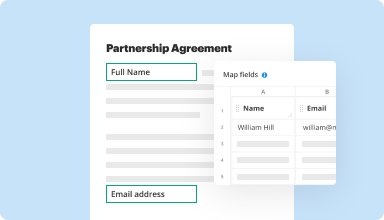
Collect data and approvals
Transform static documents into interactive fillable forms by dragging and dropping various types of fillable fields on your PDFs. Publish these forms on websites or share them via a direct link to capture data, collect signatures, and request payments.

Export documents with ease
Share, email, print, fax, or download edited documents in just a few clicks. Quickly export and import documents from popular cloud storage services like Google Drive, Box, and Dropbox.
Store documents safely
Store an unlimited number of documents and templates securely in the cloud and access them from any location or device. Add an extra level of protection to documents by locking them with a password, placing them in encrypted folders, or requesting user authentication.
Customer trust by the numbers
64M+
users worldwide
4.6/5
average user rating
4M
PDFs edited per month
9 min
average to create and edit a PDF
Join 64+ million people using paperless workflows to drive productivity and cut costs
Why choose our PDF solution?
Cloud-native PDF editor
Access powerful PDF tools, as well as your documents and templates, from anywhere. No installation needed.
Top-rated for ease of use
Create, edit, and fill out PDF documents faster with an intuitive UI that only takes minutes to master.
Industry-leading customer service
Enjoy peace of mind with an award-winning customer support team always within reach.
What our customers say about pdfFiller
See for yourself by reading reviews on the most popular resources:
There are things I still can't figure but overall, I am getting the hang of it and it seems fine. It takes a while to go between pages but that could be on my end.
2018-10-29
When I do the online fill out the form for application for a China Visa could not print out the form until I installed PDFfiller. Anyway, Thank you for your help.
2019-05-11
Everything is working
I checked out their pdf software, it's truly great, I liked it and I was ready to buy a year subscription, but all these bad reviews on line about this company made me nervous. However I signed up and now I am pleased to work with it
2018-01-19
Quick, easy, and efficient
Amazing
Makes building and filling out forms a breeze. The automation is great in making sure all information is included and correct.
I have had no bad experiences with this software thus far.
2022-09-08
Great Customer Service
Great customer service, very quick reply and they took care of my issue immediately. Highly recommend this company. I did use the service as a free trial once and it's well worth the yearly fee if you have a need for a service where you can fill out, update and/or use .pdf documents.
2021-05-26
Best Value PDF Software
I am using PDF filler to help sign documents that were sent with Adobe and therefore locked for a countersignature, date or time stamp edits, and changes to PDF documents to fix legal edits.
This software is very easy to use, gets the job done, and is extremely well priced relative to its competitors.
There are no features I dislike, it has honestly been a huge lifesaver at work as I am constantly fixing documents/changing pdf versions.
2020-10-13
Good
Good, but would be better if the cursor would line up exactly on each line with the line above. It's frustrating to have to manually line it up every time.
2020-05-29
What a time saving document access and communication method. The ability to format it to meet the inner personal business need and send is fantastic! Great job and thank you to the Creator(s)
2020-04-22
I had issues with my email to access my account. Customer Service has been outstanding with helping me to resolve the issues and provide support. Highly recommend PDFFiller !!
2024-12-13
How-to Guide
How to edit a PDF document using the pdfFiller editor:
01
Drag and drop your form to the uploading pane on the top of the page
02
Choose the Conclude Ordered Field feature in the editor's menu
03
Make the necessary edits to your file
04
Push the orange “Done" button to the top right corner
05
Rename the template if required
06
Print, share or save the template to your desktop
Conclude Ordered Field Feature
The Conclude Ordered Field feature enhances your data organization and ensures a more structured output. This tool provides a reliable way to handle your ordered fields, resulting in better performance and clarity in your projects.
Key Features
Seamless integration with existing systems
Customizable ordering options
User-friendly interface for easy access
Improved data accuracy and consistency
Real-time updates to keep information current
Potential Use Cases and Benefits
Manage data flows in large reports
Organize customer information effectively
Enhance data entry processes in apps
Support quick decision-making with clear data presentation
Facilitate compliance with data regulations
By implementing the Conclude Ordered Field feature, you can solve issues related to data mismanagement and confusion. It streamlines your workflows and boosts productivity, allowing you to focus on what matters most: achieving your goals.
For pdfFiller’s FAQs
Below is a list of the most common customer questions. If you can’t find an answer to your question, please don’t hesitate to reach out to us.
What if I have more questions?
Contact Support
What is an ordered field in math?
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Every ordered field contains an ordered subfield that is isomorphic to the rational numbers.
Is C an ordered field?
C is not an ordered field. Proof.
What is a field in real analysis?
In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers do. The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers.
Can the complex numbers be ordered?
TL;DR: The complex numbers are not an ordered field; there is no ordering of the complex numbers that is compatible with addition and multiplication. If a structure is a field and has an ordering, two additional axioms need to hold for it to be an ordered field.
Is Q an ordered field?
Every subfield of an ordered field is an ordered field with the same ordering as the original one. Since QR, it is an ordered field. The same holds true, for example, for the field Q[2]R as well.
What is an example of a field?
The set of real numbers and the set of complex numbers each with their corresponding + and * operations are examples of fields. However, some non-examples of a field include the set of integers, polynomial rings, and matrix rings.
Are the natural numbers an ordered field?
Ordered field. In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. The basic example of an ordered field is the field of real numbers, and every Dedekind-complete ordered field is isomorphic to the reals.
Are the irrational numbers an ordered field?
The irrational numbers, by themselves, do not form a field (at least with the usual operations). A field is a set (the irrational numbers are a set), together with two operations, usually called multiplication and addition. The set of irrational numbers, therefore, must necessarily be uncountable infinite.
How do you prove field axioms?
Question: If F is a field, and a, b,cF, then prove that if a+b=a+c, then b=c by using the axioms for a field.
Addition: a+b=b+a (Commutativity) a+(b+c)=(a+b)+c (Associativity)
Multiplication: ab=ba (Commutativity) a(bc)=(ab)c (Associativity)
Attempt at solution: I'm not sure where I can begin.
Why are integers not fields?
An example of a set of numbers that is not a field is the set of integers. It is an “integral domain." It is not a field because it lacks multiplicative inverses. Without multiplicative inverses, division may be impossible. Closure laws: a + b and ab are unique elements in the field.
Are the natural numbers a field?
The Natural numbers,, do not even possess additive inverses so they are neither a field nor a ring. The Integers,, are a ring but are not a field (because they do not have multiplicative inverses).
Are integers a field?
Field. A familiar example of a field is the set of rational numbers and the operations addition and multiplication. An example of a set of numbers that is not a field is the set of integers. It is an “integral domain." It is not a field because it lacks multiplicative inverses.
Are integers an ordered field?
Examples. The rational numbers Q, the real numbers R and the complex numbers C (discussed below) are examples of fields. The set Z of integers is not a field. In Z, axioms (i)-(viii) all hold, but axiom (ix) does not: the only nonzero integers that have multiplicative inverses that are integers are 1 and 1.
Is R an ordered field?
Any set which satisfies all eight axioms is called a complete ordered field. We assume the existence of a complete ordered field, called the real numbers. The real numbers are denoted by R.
Is ZA a field?
The lack of multiplicative inverses, which is equivalent to the fact that Z is not closed under division, means that Z is not a field. The smallest field containing the integers as a Sebring is the field of rational numbers.
#1 usability according to G2
Try the PDF solution that respects your time.






