Add or replace text, adjust formatting, insert legally binding eSignatures, and send documents for signing without hopping between apps.
Get the free angle pairs created by parallel lines cut by a transversal
Show details
Angle Pairs Created by Parallel Lines Cut by a Transversal For each set of angles name the angle pair and find the missing measurement x Type of angle pair Corresponding These angles are Congruent Same-Side Exterior Supplementary so. x 68 Alternate Interior Vertical so. x 106 Amazing Mathematics Key Name Period A B C D F Date Skills Practice Line and Angle Relationships 1 Use the map to answer each question* Assume the streets extend beyond the edges of the map* a* Identify all the angles...that are same-side exterior to 11. 164225 2742154223 In the diagram transversal t intersects lines p and q. Classify each pair of angles as vertical linear corresponding same-side exterior same-side interior alternate interior or alternate a* angle 1 and angle 2 d. angle 3 and angle 7 same side exterior interior Use the diagram to answer each question* vertical a* Identify the angles that are congruent to 6. x 68 Alternate Interior Vertical so. x 106 Amazing Mathematics Key Name Period A B C D...F Date Skills Practice Line and Angle Relationships 1 Use the map to answer each question* Assume the streets extend beyond the edges of the map* a* Identify all the angles that are same-side exterior to 11. 164225 2742154223 In the diagram transversal t intersects lines p and q. Classify each pair of angles as vertical linear corresponding same-side exterior same-side interior alternate interior or alternate a* angle 1 and angle 2 d. 164225 2742154223 In the diagram transversal t intersects...lines p and q. Classify each pair of angles as vertical linear corresponding same-side exterior same-side interior alternate interior or alternate a* angle 1 and angle 2 d. angle 3 and angle 7 same side exterior interior Use the diagram to answer each question* vertical a* Identify the angles that are congruent to 6. x 68 Alternate Interior Vertical so. x 106 Amazing Mathematics Key Name Period A B C D F Date Skills Practice Line and Angle Relationships 1 Use the map to answer each question*...Assume the streets extend beyond the edges of the map* a* Identify all the angles that are same-side exterior to 11. 164225 2742154223 In the diagram transversal t intersects lines p and q. Classify each pair of angles as vertical linear corresponding same-side exterior same-side interior alternate interior or alternate a* angle 1 and angle 2 d. angle 3 and angle 7 same side exterior interior Use the diagram to answer each question* vertical a* Identify the angles that are congruent to 6.
We are not affiliated with any brand or entity on this form
Fill out, sign, and share forms from a single PDF platform
Manage all your documents quickly and securely in the cloud.
Edit and sign in one place
Create professional forms
Add and customize fillable fields to tailor each form to your needs and ensure easy completion without printing and scanning.
Simplify data collection
Quickly share forms via email or a secure link, enabling anyone to complete forms online in seconds, on any device.
Manage forms centrally
Keep all your forms and templates organized in one secure, cloud-based platform, track changes easily, and export documents in any format.
Why pdfFiller is the best tool for your documents and forms
End-to-end document management
From editing and signing to collaboration and tracking, pdfFiller has everything you need to get your documents done quickly and efficiently.
Accessible from anywhere
pdfFiller is fully cloud-based. This means you can edit, sign, and share documents from anywhere using your computer, smartphone, or tablet.
Secure and compliant
pdfFiller lets you securely manage documents following global laws like ESIGN, CCPA, and GDPR. It's also HIPAA and SOC 2 compliant.
Understanding Angle Pairs and Their Relationships
What are angle pairs created by parallel lines cut by a transversal?
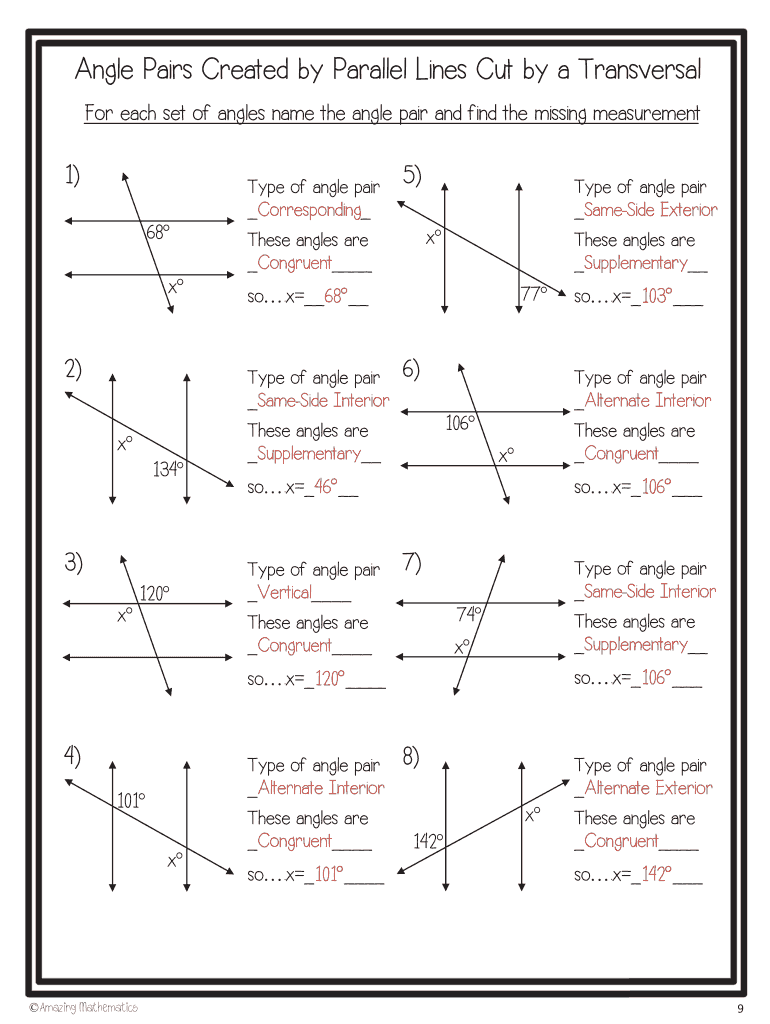
Angle pairs created by parallel lines cut by a transversal are specific relationships that arise when two parallel lines are intersected by another line, called a transversal. This setup generates several types of angle pairs, including corresponding angles, alternate interior angles, alternate exterior angles, same-side interior angles, and same-side exterior angles. Each has unique properties that govern their measurements, often classified as either congruent or supplementary. Understanding these properties is essential for solving geometric problems and proofs.
Key Characteristics of Angle Pair Relationships
The characteristics of angle pairs created by parallel lines include: congruency and supplementarity. Corresponding angles are congruent; same-side interior and same-side exterior angles are supplementary. These angle relationships provide a systematic approach to determining angle measures, making problem-solving simpler in geometry. Identifying and utilizing these relationships effectively can lead to accurate conclusions and proofs in mathematical tasks.
When to Use Angle Pair Relationships
Angle pair relationships are beneficial when analyzing geometric figures, particularly in determining unknown angle measures in various applications. This includes tasks such as completing worksheets focused on angle pair relationships, proof formulation, or solving real-life problems involving parallel lines and transversals. Understanding when to employ these relationships is crucial for enhancing comprehension and improving accuracy in geometric studies.
Best Practices for Accurate Angle Measurement
Accuracy in measuring angles is vital for drawing correct conclusions in geometry. To ensure precision, label angles thoroughly and consistently within diagrams. When working with angle pairs, it is important to apply the correct relationships and methods for calculations. Additionally, double-check your work for any potential oversight. Familiarizing yourself with multiple example problems can reinforce your understanding and improve your problem-solving skills.
Common Errors and Troubleshooting
Errors can arise when classifying angle pairs or applying the properties of angle relationships incorrectly. Common mistakes include misidentifying corresponding or alternate interior angles and confusion between supplementary and congruent angles. To troubleshoot these issues, review the classifications of angle pairs, refer to geometric principles, and practice with various problems. Such strategies will strengthen your understanding and reduce the likelihood of errors in future calculations.
Benefits of Understanding Angle Pair Relationships
Grasping the concept of angle pairs created by parallel lines cut by a transversal enhances analytical skills in geometry. This knowledge facilitates easier identification of angle relationships, leading to quicker problem-solving and improved accuracy in mathematical reasoning. Such foundational skills are applicable in both academic settings and real-life scenarios, providing tools for evaluating angles effectively.
Frequently Asked Questions about parallel lines cut by a transversal worksheet form
What types of angle pairs are created by parallel lines and a transversal?
The types of angle pairs include corresponding angles, alternate interior angles, alternate exterior angles, same-side interior angles, and same-side exterior angles.
Why are angle pairs important in geometry?
Angle pairs are important because they help establish relationships between angles, which can be used to solve geometric problems and proofs.
How can I ensure accurate identification of angle pairs?
To ensure accurate identification, label angles clearly in diagrams and familiarize yourself with the characteristics and classifications of different angle pairs.
pdfFiller scores top ratings on review platforms
Great for a small volume rental business.
I like it. just a little bit slow. mobile app needs development
People Also Ask about parallel lines cut by a transversal worksheet with answers pdf
What is a pair of parallel lines cut by a transversal?
If two parallel lines are cut by a transversal, then, Alternate Exterior Angles are congruent. If two parallel lines are cut by a transversal, then corresponding angles are congruent.
How to do angle pairs created by parallel lines cut by a transversal?
0:05 2:09 Angle Pairs-Parallel Lines Cut by a Transversal - YouTube YouTube Start of suggested clip End of suggested clip Let's look at parallel lines cut by a transversal. Line so remember angle 1 and angle 2 areMoreLet's look at parallel lines cut by a transversal. Line so remember angle 1 and angle 2 are supplementary which means they have to add up to 180.
How many angles are formed by a transversal with a pair of parallel lines?
8 angles are formed when a transversal cuts two parallel lines.
How do you solve parallel lines cut by a transversal equation?
1:51 8:50 Solving Problems Involving Parallel Lines Cut by a Transversal YouTube Start of suggested clip End of suggested clip If two parallel lines are caught by transversal therefore same side interior angles areMoreIf two parallel lines are caught by transversal therefore same side interior angles are supplementary if they are supplementary. We can create an equation.
How do you solve parallel lines cut by transversal?
1:51 8:50 Solving Problems Involving Parallel Lines Cut by a Transversal YouTube Start of suggested clip End of suggested clip If two parallel lines are caught by transversal therefore same side interior angles areMoreIf two parallel lines are caught by transversal therefore same side interior angles are supplementary if they are supplementary. We can create an equation. Like this we have 2x minus 7 plus 3x plus 12
How to solve angles formed by parallel lines cut by a transversal?
1:44 5:55 Angles Formed by a Transversal with Two Parallel Lines | Don't Memorise YouTube Start of suggested clip End of suggested clip When a transversal intersects a pair of parallel lines. Four pairs of corresponding. Angles areMoreWhen a transversal intersects a pair of parallel lines. Four pairs of corresponding. Angles are formed two. And six form a corresponding angles pair. So angle two will always equal angle.
Related pages
Related to angle pairs created by
If you believe that this page should be taken down, please follow our DMCA take down process
here
.
This form may include fields for payment information. Data entered in these fields is not covered by PCI DSS compliance.