Get the free Orthocenter and Incenter Date - Geometry CC

Name: ___Date: ___Period: ___Chapter 3: Constructions Topic 5: Orthocenter, Circumcenter & CircumcircleConstruction #9: Orthocenter All three ALTITUDES The orthocenter is found at the intersection of all three ___ in a triangle. To construct the altitudes, construct a perpendicular line through the side of the triangle from the opposite vertex (use construction #8b point off the line). The altitudes of a triangle, extended if necessary, are concurrent in a point called the ___ of the triangle

How to fill out orthocenter and incenter date

How to fill out orthocenter and incenter date

1. Identify the triangle for which you need to find the orthocenter and incenter.
2. For the orthocenter: Find the slopes of each side of the triangle.
3. Calculate the equations of the altitudes by determining the perpendicular lines from each vertex to the opposite side.
4. Locate the point where the three altitudes intersect; this point is the orthocenter.
5. For the incenter: Measure the lengths of the sides of the triangle.
6. Use the angle bisectors from each vertex to find the intersection point.
7. The intersection point of the angle bisectors is the incenter, which is also the center of the inscribed circle.

Who needs orthocenter and incenter date?

1. Students studying geometry who need to understand triangle properties.
2. Architects and engineers who require precise calculations for constructions involving triangles.
3. Mathematicians and researchers involved in geometric studies.
4. Anyone working in fields that require triangulation or optimization, such as navigation or robotics.

Orthocenter and Incenter Date Form: A Comprehensive Guide

Understanding triangle centers: An overview

Triangle centers, such as the orthocenter and incenter, play a crucial role in geometry, serving as key points that enhance our understanding of triangle properties. Each triangle center provides unique insights that aid in both mathematical theory and real-world applications, ranging from architecture to computer graphics. By comprehensively analyzing these centers, we can uncover geometrical relationships that enrich our problem-solving capabilities.

• Understanding relationships: Grasping how triangle centers interplay can help in solving complex geometric problems.
• Applications: The orthocenter and incenter are pivotal in practical scenarios, such as construction and design.
• Mathematical importance: These centers allow deeper insight into the nature and properties of triangles.

What is an orthocenter?

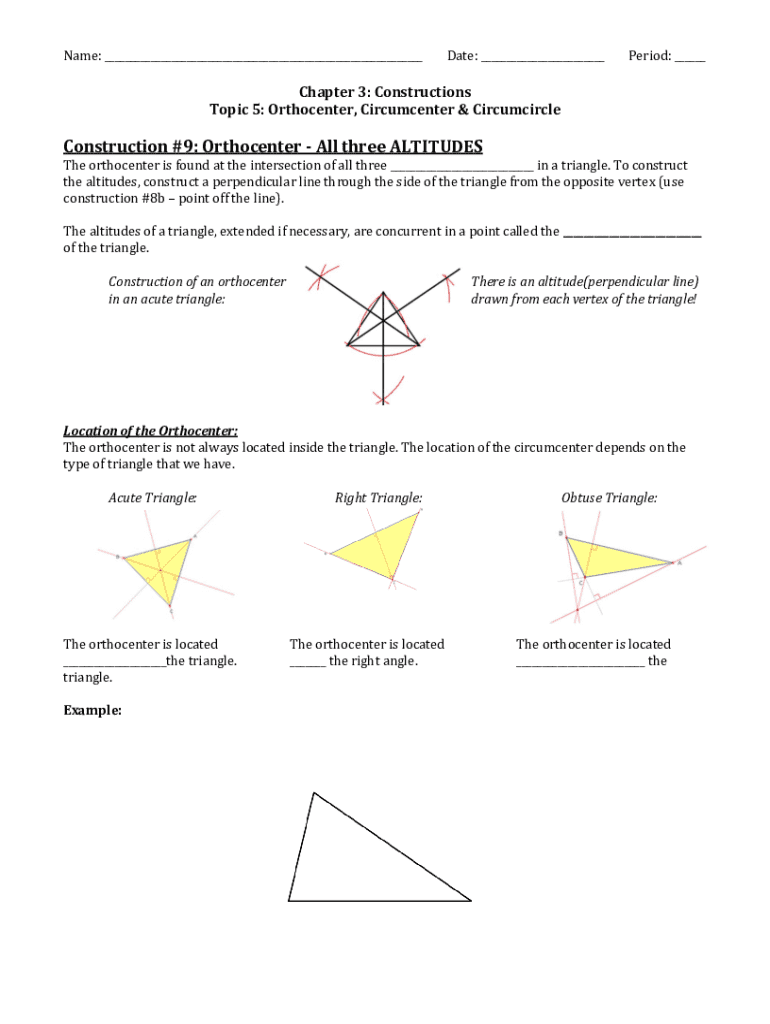
The orthocenter of a triangle is defined as the point where the three altitudes intersect. An altitude of a triangle is a perpendicular segment from a vertex to the line containing the opposite side. This geometric property makes the orthocenter a unique point that varies depending on whether the triangle is acute, right, or obtuse. The orthocenter is an essential aspect in various geometric proofs and discussions concerning triangle properties.

To locate the orthocenter, follow these steps: First, draw the altitudes from each vertex to the opposite side. Identify where each altitude meets the line of the opposite side; these points are the feet of the altitudes. Finally, the intersection of all three altitudes, known as the point of concurrency, is the orthocenter. Understanding how to find the orthocenter is vital for anyone studying triangle properties more deeply.

• Draw the first altitude: Choose a vertex and draw a perpendicular line to the opposite side.
• Repeat for the remaining two vertices, ensuring proper perpendicular alignment.
• Mark the point where all three altitudes intersect; this is the orthocenter.

In the real world, the orthocenter's applications range from navigation systems that utilize triangulation methods to architectural designs prioritizing stability and aesthetic value. The orthocenter's insights can provide necessary data for engineers and architects.

What is an incenter?

The incenter of a triangle is defined as the point where the angle bisectors of the three angles of the triangle intersect. It is equidistant from all three sides of the triangle. The incenter is vital in geometry, as it is the center of the incircle—the circle that can be inscribed within the triangle. The properties of the incenter highlight the symmetry and balance that triangles possess.

To locate the incenter, follow these steps: Draw the angle bisectors for each angle of the triangle. The intersections of these bisectors will converge at a single point—the incenter. This point then serves as the center of the incircle, illustrating the relationship between angle bisectors and triangle dimensions.

• Construct the first angle bisector: Start from one angle and draw a line that divides it into two equal angles.
• Repeat the process with the remaining two angles to find their respective bisectors.
• Identify the point where all three angle bisectors meet; this intersection is the incenter.

Practical applications of the incenter are vast and include fields like architecture—specifically relating to the planning of circular designs—and in various aviation applications where precise angles relate to fuel efficiency and trajectory.

Detailed comparison: orthocenter vs. incenter

While both the orthocenter and incenter are defined as points of concurrency within a triangle, they hold distinct properties. The orthocenter focuses on altitudes and emphasizes overall height, while the incenter is derived from angle bisectors and centers around equilibrium and side distance consistency. Understanding these differences can significantly enhance our problem-solving toolkit when dealing with triangles.

In terms of situational usage, the orthocenter is particularly useful when analyzing relationships in acute and obtuse triangles, while the incenter is essential for computations related to circle properties. The following table encapsulates their key differences:

• Found at the intersection of altitudes; varies with triangle type.
• Found at the intersection of angle bisectors; equidistant from triangle sides.

Interaction between orthocenter and incenter

The relationship between the orthocenter and incenter reveals much about the nature of triangles themselves. For example, in acute triangles, the orthocenter lies within the triangle, while for obtuse triangles, it is located outside. Despite their different positions, both centers contribute to the overall balance of the triangle in different geometric contexts.

The centroid, the intersection of the medians, also plays a critical role in this interaction by serving as a balancing point for the triangle. Visualizing these interactions can provide profound insights into triangle geometry, often facilitating easier construction and rigorous geometric proofs.

• All concurrency points (orthocenter, incenter, and centroid) are within the triangle.
• The orthocenter resides outside the triangle, while the centroid and incenter remain inside.
• The orthocenter coincides with one vertex; the incenter is within the triangle.

Calculating coordinates of orthocenter and incenter

To derive the coordinates of the orthocenter and incenter, one must utilize the triangle's vertices as a foundation. For the orthocenter, applying the equations of the altitudes can be done through coordinate geometry, whereby the point of intersection is calculated. For the incenter, the coordinates can be derived using the angle bisector theorem and the distances from each vertex to the opposite side.

Here's how to calculate these coordinates step-by-step: First, identify the vertices of the triangle using their coordinates (x1, y1), (x2, y2), and (x3, y3). For the orthocenter, derive equations for each altitude and solve for intersection points. For the incenter, compute the respective angle bisectors' equations, gather the necessary perpendicular distances and solve for coordinates accordingly.

• Identify the coordinates of the triangle's vertices.
• Calculate the altitudes and angle bisectors.
• Solve the equations simultaneously to find points of concurrency.

Common pitfalls in these calculations often involve misidentifying points or making computational errors; therefore, it is crucial to double-check calculations and ensure clarity in each mathematical step.

Tools for creating and managing orthocenter and incenter data forms

When working with geometric concepts and documentation, using tools like pdfFiller for creating orthocenter and incenter data forms can substantially streamline the process. With pdfFiller's cloud-based platform, users are empowered to create, edit, and manage PDF documents for geometric studies with ease.

Creating personalized forms allows students and professionals to efficiently document their findings, calculations, and data related to triangle centers, enhancing collaboration or sharing with peers and expert review.

• Interactive form creation functionality tailored to triangle center studies.
• Easy-to-use editing tools for adjusting content and formatting.
• Signing and sharing functionalities to promote collaboration among teams.

Practical instructions for using the orthocenter and incenter form

Filling out the orthocenter and incenter data form on pdfFiller is straightforward. Start by gathering all necessary triangle vertex coordinates and required angles. Next, input these details into the designated fields of the form. Ensure accuracy to facilitate proper calculations of both centers.

Collaboration on geometric projects becomes seamless with the shared editing feature available in pdfFiller. This allows for joint efforts on triangle geometry-related assignments, optimizing the learning experience and ensuring thorough understanding.

• Double-check all entries for accuracy.
• Utilize collaboration tools for group projects.
• Apply proper notations throughout documents for clarity.

Case studies: successful applications of triangle centers

Triangle centers have been applied successfully across various fields, reflecting their significance. In architecture, the principles underlying the orthocenter and incenter guide design choices, ensuring structural integrity while achieving artistic vision. Furthermore, in computational geometry, algorithms making use of triangle centers optimize processing in computer graphics and simulations.

Testimonials from educators reveal the effectiveness of using orthocenters and incenters to better illustrate mathematical concepts, with students showcasing improved understanding through practical application. Case studies undeniably show the versatile usage of these geometric principles across disciplines.

• Architectural designs utilizing the balance provided by the orthocenter.
• Computational algorithms where triangle centers enhance data processing efficiency.
• Educational methodologies incorporating triangle centers for improved student engagement.

Engaging with triangle centers: activities and exercises

Engaging with triangle centers through interactive activities enhances understanding and retention. For instance, consider implementing a coloring activity where students identify and label the orthocenter and incenter in various types of triangles. Such activities not only reinforce knowledge but also promote creativity.

Furthermore, interactive worksheets can be developed with problems centered around the calculation of these triangle centers. Group projects encouraging hands-on exploration of concurrency points can facilitate collaborative learning and deepen comprehension of triangular properties.

• Coloring exercise to identify orthocenter and incenter.
• Worksheets featuring problems on triangle center calculations.
• Group projects focused on researching triangle properties.

Frequently asked questions (FAQ) about orthocenter and incenter

As studies on triangle centers progress, common inquiries arise that warrant clarification. Understanding the importance of each type of triangle—acute, obtuse, and right—and their respective orthocenter and incenter positions is essential. Additionally, advanced questions often probe into the implications of triangle centers in broader mathematical theories.

Addressing these queries can empower learners and stimulate their interest in diving deeper into triangle geometry. Engagement with these questions fosters a conducive environment for discovering mathematical truths and developing problem-solving skills.

• What are the properties of the orthocenter and incenter in different triangle types?
• How do orthocenter and incenter relate to each other?
• Can the orthocenter and incenter be equidistant from vertices?

Summary of key concepts

The exploration of orthocenter and incenter provides immense value in geometry, offering insights into triangle properties and their practical applications. Recognizing the intersections between these triangle centers enables a deeper understanding of geometric relationships that extend into various fields, from architecture to mathematics education.

This guide encourages learners and professionals alike to utilize the tools on pdfFiller for seamless document management in their geometric explorations, enhancing their ability to capture and analyze important data surrounding triangle centers effectively.

For pdfFiller’s FAQs

How can I edit orthocenter and incenter date on a smartphone?

The easiest way to edit documents on a mobile device is using pdfFiller’s mobile-native apps for iOS and Android. You can download those from the Apple Store and Google Play, respectively. You can learn more about the apps here. Install and log in to the application to start editing orthocenter and incenter date.

Can I edit orthocenter and incenter date on an Android device?

The pdfFiller app for Android allows you to edit PDF files like orthocenter and incenter date. Mobile document editing, signing, and sending. Install the app to ease document management anywhere.

How do I fill out orthocenter and incenter date on an Android device?

Complete orthocenter and incenter date and other documents on your Android device with the pdfFiller app. The software allows you to modify information, eSign, annotate, and share files. You may view your papers from anywhere with an internet connection.

What is orthocenter and incenter date?

The orthocenter refers to the point where the three altitudes of a triangle intersect, while the incenter is the point where the angle bisectors meet, determining the center of the triangle's incircle.

Who is required to file orthocenter and incenter date?

Filing for orthocenter and incenter date is not a standard requirement and may refer to specialized contexts or applications in geometry. Typically, individuals or entities involved in mathematical research or education might engage with these concepts.

How to fill out orthocenter and incenter date?

Filling out orthocenter and incenter date would typically involve calculating the coordinates of the orthocenter and incenter based on the vertices of the triangle and providing relevant geometric details as required in a specific context.

What is the purpose of orthocenter and incenter date?

The purpose of orthocenter and incenter date is to document and utilize geometric properties in mathematical studies, applications in design, or computations requiring the properties of triangles.

What information must be reported on orthocenter and incenter date?

The information that must be reported includes the coordinates of the orthocenter and incenter, the vertices of the triangle, and any calculations or formulas used in determining these points.