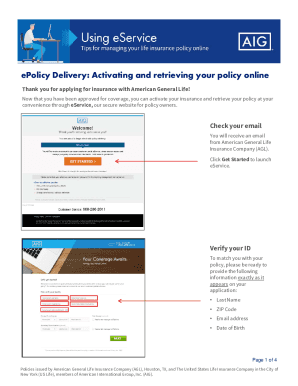
Get the free Nmeros ordinais: o que so e lista com os principais ...

NO. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112English 2D/3D TYPE Emulator Attack of the Movies 3D 3D LIGHTGUN WII Dino Strike 3D LIGHTGUN WII Ghost Squad 3D LIGHTGUN WII GunBlade N.Y & L.A....

How to fill out nmeros ordinais o que

How to fill out nmeros ordinais o que

1. Identify the ordinal number you wish to write.
2. Start with the base number and add the appropriate suffix.
3. Use ' primeiro' for first, ' segundo' for second, ' terceiro' for third, and so on.
4. Be mindful of gender agreement: use 'primeira' for feminine nouns.
5. For numbers above 10, use ' décimo' for 10th, ' vigésimo' for 20th, etc.
6. Write the ordinal number in the context of the sentence, ensuring grammatical correctness.

Who needs nmeros ordinais o que?

1. Students studying Portuguese grammar.
2. Anyone learning to express rankings or orders in conversations.
3. Individuals writing formal documents requiring ordinal numbers.
4. Teachers preparing educational materials.
5. Translators converting texts that include rankings.

Números ordinais e o que form

Definição de números ordinais

Números ordinais são usados para indicar a posição ou a ordem de elementos dentro de um conjunto. Por exemplo, em uma corrida, o primeiro, segundo e terceiro colocado são designados por números ordinais. A principal diferença entre números ordinais e números cardinais reside no fato de que os ordinais expressam ordem, enquanto os cardinais quantificam. Os números cardinais são usados para contar, enquanto os ordinais são cruciais para classificar.

• Indica o primeiro lugar como um número ordinal.
• Indica o segundo lugar na classificação.

Propriedades dos números ordinais

Os números ordinais podem ser divididos em ordinais finitos e ordinais infinitos. Os ordinais finitos incluem sequências como 1º, 2º, 3º e assim por diante, enquanto os ordinais infinitos incluem tipos como 'ω' (ômega), que representa o menor número ordinal infinito. A teoria de ordinais de Von Neumann é um dos fundamentos da matemática, definindo ordinais em termos de conjuntos. Cada número ordinal é representado como o conjunto de todos os ordinais menores que ele.

• Um número ordinal que é um número natural como 1, 2, 3.
• Um número ordinal que não é finito, como ω.

Sequência dos números ordinais

Os números ordinais têm uma ordem bem definida, onde cada ordinal é comparável ao outro. Por exemplo, 3º é menor que 4º. Para representar números ordinais, frequentemente utilizamos uma notação que inclui a posição e, em alguns casos, um subscrito para indicar o tipo de ordinal. Visualmente, isso pode ser entendido através de diagramas, onde ordinais são colocados em uma linha do tempo que indica sua sequência. Essa representação ajuda a clarificar a relação entre diferentes ordinais.

• O primeiro em uma série.
• O segundo em uma série.
• O terceiro em uma série.

Aritmética de números ordinais

As operações básicas com números ordinais incluem adição, subtração e multiplicação, mas diferentemente dos números cardinais, a aritmética de ordinais não é tão simples. Por exemplo, ao somar ordinais, a ordem dos operandos importa, ou seja, '2º + 1º = 3º', mas '1º + 2º' pode resultar em uma sequência diferente, como '2º'. Essas operações possuem propriedades únicas que diferem de princípios matemáticos usuais, sendo importante entender as regras específicas que regem a aritmética ordinal.

• A soma de ordinais não é comutativa.
• Uma operação mais complexa e, em muitos casos, não é definida.

Uso de números ordinais em outros campos

Os números ordinais têm uma presença significativa na teoria dos conjuntos, onde são usados para classificar e organizar elementos de conjuntos bem ordenados. Por exemplo, em ciências da computação, a estrutura de dados pode ser baseada em ordenações que utilizam números ordinais para rotular os níveis hierárquicos de dados. Adicionalmente, na topologia, números ordinais ajudam na definição de espaços, orientando diversas propriedades topológicas que dependem da relação de ordem entre os conjuntos.

• Ordem dos elementos em conjuntos bem definidos.
• Utilização de ordinais na definição de espaços.

Ordinais sucessor e limite

Ordinais sucessores são aqueles que seguem diretamente outro ordinal, como 1º sendo seguido por 2º. Já os ordinais limite, como ω, não possuem um sucessor imediato; eles representam o conceito de 'infinito' em uma sequência. Esses ordinais limites são essenciais para a compreensão de muitas propriedades em matemática, especialmente na análise de sequências e operações infinitas.

• O próximo ordinal após um dado ordinal.
• Ordinais que não têm um sucessor, como ω.

A indução transfinita

Indução transfinita é um método de prova que estende o princípio da indução matemática a números ordinais. Este conceito permite que se prove propriedades que se aplicam a todos os ordinais, utilizando uma base e um passo indutivo que se aplica a ordinais sucessores e limites. Esta técnica é fundamental em teorias matemáticas complexas, permitindo uma dedução ampla e aplicável em muitos contextos.

• Método para provar propriedades sobre números ordinais.
• Aplicações da indução transfinita em teoremas da matemática.

Ordinais contáveis e não contáveis

Ordinais contáveis são aqueles que podem ser listados em sequência infinita, como 1º, 2º, 3º, enquanto os ordinais não contáveis representam ordinais que não podem ser enumerados, como ℵ₁ (alef um). Essa diferença é crucial na compreensão de grandes conjuntos e suas propriedades no âmbito da matemática. Ordinais 'enormes', como os discutidos na Teoria da Grandeza, trazem questões intrigantes sobre a estrutura e a fundação da matemática em dimensões mais abstratas.

• Ordinais que podem ser listados em uma sequência infinita.
• Ordinais que não podem ser listados, como ℵ₁.

Ordenação de conjuntos com ordinais

A ordenação de conjuntos utilizando números ordinais permite uma classificação clara e eficiente. Técnicas para classificar conjuntos incluem a atribuição de ordinais a cada elemento com base na sua posição relativa, formando conjuntos bem ordenados. Essa abordagem é fundamental em diversas áreas da matemática, pois garante a consistência da estrutura dos conjuntos e facilita a análise e a comparação de seus elementos.

• Utilização de ordinais para classificar e organizar conjuntos.
• Exemplos de como ordinais asseguram a ordem em conjuntos.

Classificações e estruturas

A estrutura de classes em matemática permite uma compreensão mais profunda de como ordinais e cardinais se inter-relacionam. Enquanto os ordinais expressam a ordem dos elementos, os cardinais oferecem uma visão sobre a quantidade. A comparação entre ordinais e cardinais ajuda os matemáticos a entender melhor a natureza dos números e suas propriedades, destacando a importância dos ordinais na criação de estruturas matemáticas complexas.

• Estruturas que utilisent ordinais para definir propriedades em matemática.
• Diferenças fundamentais entre ordinais e números cardinais.

Ordinais na teoria das categorias

Em teoria das categorias, os números ordinais desempenham um papel crucial na definição de classes de equivalência. Eles ajudam a estruturar as relações entre diferentes objetos matemáticos, proporcionando um framework para compreender como diferentes categorias estão interconectadas. A intersecção de ordinais dentro de várias estruturas matemáticas enriquece a análise e a argumentação, oferecendo uma nova dimensão à pesquisa em matemática.

• Definição e papel dos ordinais na estruturação dessa relação.
• Relevância dos ordinais em diferentes disciplinas e sua aplicação nos métodos de prova e discussão.

Conclusões sobre números ordinais

Fica evidente que os números ordinais não são apenas uma curiosidade matemática, mas um pilar fundamental na construção do conhecimento matemático moderno. Sua aplicação se estende por várias áreas, desde a teoria dos conjuntos até a topologia e a teoria das categorias. À medida que novas pesquisas exploram o domínio dos ordinais, novos conceitos e aplicações continuarão a surgir, prometendo evoluções na compreensão básica da matemática.

• Importância dos números ordinais na matemática contemporânea.
• Perspectivas de pesquisa e estudo em áreas envolvendo ordinais.

Perguntas frequentes sobre números ordinais

Muitas pessoas se questionam como os números ordinais se aplicam em situações práticas. Eles são usados em classificações de rankings, listas de espera e na organização de dados em computação. A diferença essencial entre números ordinais e números naturais é que os ordinais expressam uma posição específica, enquanto os naturais apenas indicam uma contagem. Este entendimento é crucial para aqueles que utilizam documentos e dados, especialmente em plataformas como pdfFiller, onde a organização da informação é fundamental.

• Ordinais utilizados em rankings e classificações.
• Números ordinais versus números naturais.

Anexos e notas finais

Para uma compreensão mais abrangente, é útil um glossário de termos relacionados, como 'ordinal', 'cardinal', 'infinitos' e 'limite'. Somado a isso, exemplos práticos de uso de ordinais, como em classificações de resultados esportivos ou na organização de informações através de ferramentas digitais, como o pdfFiller, podem enriquecer o aprendizado e a aplicação prática de conceitos. Com essas informações, os leitores podem se aprofundar ainda mais na riqueza do tema dos números ordinais.

• Termos fundamentais para o entendimento de números ordinais.
• Aplicações de ordinais na vida real e em documentos.

For pdfFiller’s FAQs

How can I edit nmeros ordinais o que from Google Drive?

Using pdfFiller with Google Docs allows you to create, amend, and sign documents straight from your Google Drive. The add-on turns your nmeros ordinais o que into a dynamic fillable form that you can manage and eSign from anywhere.

How do I make edits in nmeros ordinais o que without leaving Chrome?

Get and add pdfFiller Google Chrome Extension to your browser to edit, fill out and eSign your nmeros ordinais o que, which you can open in the editor directly from a Google search page in just one click. Execute your fillable documents from any internet-connected device without leaving Chrome.

Can I edit nmeros ordinais o que on an Android device?

You can edit, sign, and distribute nmeros ordinais o que on your mobile device from anywhere using the pdfFiller mobile app for Android; all you need is an internet connection. Download the app and begin streamlining your document workflow from anywhere.

What is nmeros ordinais o que?

Números ordinais are numbers that indicate the order of items in a sequence, such as first, second, third, etc.

Who is required to file nmeros ordinais o que?

Those who need to report or organize items in a sequential manner, such as in competitions or lists, may be required to use números ordinais.

How to fill out nmeros ordinais o que?

To fill out números ordinais, write the number followed by the appropriate ordinal indicator, such as '1st', '2nd', '3rd', or '4th'.

What is the purpose of nmeros ordinais o que?

The purpose of números ordinais is to denote positions or rankings in a set, helping to convey order and hierarchy.

What information must be reported on nmeros ordinais o que?

The information reported should include the item or entity being ranked and its corresponding ordinal number.