Call For Ordered Field For Free
Drop document here to upload
Up to 100 MB for PDF and up to 25 MB for DOC, DOCX, RTF, PPT, PPTX, JPEG, PNG, JFIF, XLS, XLSX or TXT
Note: Integration described on this webpage may temporarily not be available.
0
Forms filled
0
Forms signed
0
Forms sent
Discover the simplicity of processing PDFs online
Upload your document in seconds
Fill out, edit, or eSign your PDF hassle-free
Download, export, or share your edited file instantly
Top-rated PDF software recognized for its ease of use, powerful features, and impeccable support
Every PDF tool you need to get documents done paper-free
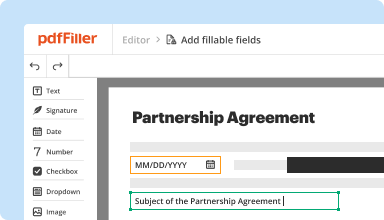
Create & edit PDFs
Generate new PDFs from scratch or transform existing documents into reusable templates. Type anywhere on a PDF, rewrite original PDF content, insert images or graphics, redact sensitive details, and highlight important information using an intuitive online editor.
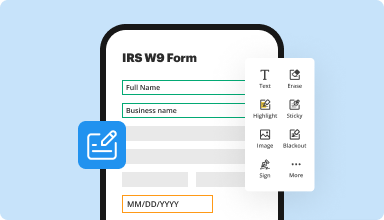
Fill out & sign PDF forms
Say goodbye to error-prone manual hassles. Complete any PDF document electronically – even while on the go. Pre-fill multiple PDFs simultaneously or extract responses from completed forms with ease.
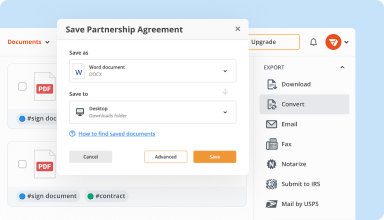
Organize & convert PDFs
Add, remove, or rearrange pages inside your PDFs in seconds. Create new documents by merging or splitting PDFs. Instantly convert edited files to various formats when you download or export them.
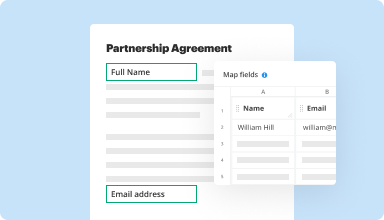
Collect data and approvals
Transform static documents into interactive fillable forms by dragging and dropping various types of fillable fields on your PDFs. Publish these forms on websites or share them via a direct link to capture data, collect signatures, and request payments.
Export documents with ease
Share, email, print, fax, or download edited documents in just a few clicks. Quickly export and import documents from popular cloud storage services like Google Drive, Box, and Dropbox.
Store documents safely
Store an unlimited number of documents and templates securely in the cloud and access them from any location or device. Add an extra level of protection to documents by locking them with a password, placing them in encrypted folders, or requesting user authentication.
Customer trust by the numbers
64M+
users worldwide
4.6/5
average user rating
4M
PDFs edited per month
9 min
average to create and edit a PDF
Join 64+ million people using paperless workflows to drive productivity and cut costs
Why choose our PDF solution?
Cloud-native PDF editor
Access powerful PDF tools, as well as your documents and templates, from anywhere. No installation needed.
Top-rated for ease of use
Create, edit, and fill out PDF documents faster with an intuitive UI that only takes minutes to master.
Industry-leading customer service
Enjoy peace of mind with an award-winning customer support team always within reach.
What our customers say about pdfFiller
See for yourself by reading reviews on the most popular resources:
Was looking for a fast PDF fillable form. I found it here. Even has e-sign which really makes me look professional. Always wanted to try it and now I'm glad I did.
2016-05-27
the service is great, however the payment option is miss leading, as it says $6/month and when you go to pay you charge the full year up front, in US$ and some of us are poor, so thanks for that.
2018-03-16
Excellent Software and a great price
Very good and have used it for years.
PDF filler works so well and make it so easy to fill out forms online. It works and the price is very reasonable. I use this for all of my documents as it saves me time.
I can't think of a negative with the software, it always works and has a range of features which are constantly getting better.
2018-10-20
This software has solved many problems for a few clients, well done.
Being able to host the forms online for anyone to fill out, which is something that I couldn't find with any other software.
No way to remove the flow of fields, you are just able to move the order around, which is very annoying as well.
2017-11-14
Hello:) This is an incredible…
Hello:) This is an incredible experience of communicating with online help. Thanks Kara's did me a big favor by helping me figure out the site.
I wish her and the company only heights and be happy and prosperous!
2023-05-23
Expensive for irregular user but overall excellent!
Expensive if you are an occasional user, and I wish the "fill in the blanks" were a little more automatic with alignment. But overall excellent!
2023-04-04
Support Service:
Support Service:
I reported an issue to support team and the response was automatic and the issue was resolved immediately.
Excellent service and a fantastic support team!!!
10/10 Well done...
2022-03-04
I finally got it to work however when I…
I finally got it to work however when I had it opened on a different browser I couldn't get it to do some stuff I was trying to get it to do and why do I have to pay more for faxing?
2021-05-14
Their customer service is great! Joyce helped me out and was super helpful and considerate! Best customer service experience I’ve had. Thanks for the quick response!
2020-05-03
How-to Guide
How to edit a PDF document using the pdfFiller editor:
01
Drag and drop your template using pdfFiller`s uploader
02
Select the Call For Ordered Field features in the editor`s menu
03
Make all the necessary edits to the file
04
Click the orange “Done" button to the top right corner
05
Rename the template if necessary
06
Print, email or save the form to your device
Call For Ordered Field Feature
The Call For Ordered Field feature enhances your data collection process by allowing you to precisely control the order of fields in your calls. This streamlined approach ensures you gather the right information when you need it, making it invaluable for businesses that depend on accurate data.
Key Features
Customizable field arrangement for tailored data collection
Easy integration with existing systems
User-friendly interface for seamless navigation
Real-time updates for immediate access to data
Reliable support for troubleshooting and queries
Potential Use Cases and Benefits
Optimizing surveys and questionnaires to improve response rates
Streamlining sales calls to capture essential customer information
Enhancing customer support interactions for more efficient service
Improving data accuracy in research and analysis projects
Facilitating onboarding processes with structured data collection
This feature resolves common data collection challenges. By allowing you to dictate the order in which fields appear, you minimize confusion and enhance clarity. Users can focus on one piece of information at a time, leading to higher quality data. Whether you are conducting a survey, making a sales call, or providing customer support, this feature adapts to your needs. Invest in the Call For Ordered Field feature to gain control over your data collection and improve the overall efficiency of your operations.
For pdfFiller’s FAQs
Below is a list of the most common customer questions. If you can’t find an answer to your question, please don’t hesitate to reach out to us.
What if I have more questions?
Contact Support
Are rational numbers an ordered field?
By Rational Numbers form Field, (Q, +,×) is a field. By Total Ordering on Quotient Field is Unique, it follows that (Q, +,Ã) has a unique total ordering on it that is compatible with its ring structure. Thus, (Q,+,Ã,) is a totally ordered field.
Are the irrational numbers an ordered field?
The irrational numbers, by themselves, do not form a field (at least with the usual operations). A field is a set (the irrational numbers are a set), together with two operations, usually called multiplication and addition. The set of irrational numbers, therefore, must necessarily be uncountable infinite.
Is Zero is a rational number?
Yes zero is a rational number. We know that the integer 0 can be written in any one of the following forms. Thus, 0 can be written as, where a/b = 0, where a = 0 and b is any non-zero integer. Hence, 0 is a rational number.
Are the complex numbers an ordered field?
Every ordered field is a formally real field, i.e., 0 cannot be written as a sum of nonzero squares. The complex numbers also cannot be turned into an ordered field, as 1 is a square (of the imaginary number i) and would thus be positive.
Are positive numbers a field?
The positive-real numbers can also form a field, (R>0,), with the operation xy=eln(x)ln(y) for all x, yR>0. Here, all positive-real numbers except 1 are the “multiplicative" units, and thus R>0={xR>0×1}.
Can complex numbers be compared?
Among any two integers or real numbers one is larger, another smaller. But you can't compare two complex numbers. (a + IB) < (c + id), The same is true for complex numbers as well.
What is the point of complex numbers?
Imaginary numbers, also called complex numbers, are used in real-life applications, such as electricity, as well as quadratic equations. In quadratic planes, imaginary numbers show up in equations that don't touch the x-axis. Imaginary numbers become particularly useful in advanced calculus.
What is field with example?
The set of real numbers and the set of complex numbers each with their corresponding + and * operations are examples of fields. However, some non-examples of a field include the set of integers, polynomial rings, and matrix rings.
How do you prove something is a field?
Suggested clip
Linear Algebra: Prove a set of numbers is a field — YouTubeYouTubeStart of suggested clipEnd of suggested clip
Linear Algebra: Prove a set of numbers is a field — YouTube
Is R an ordered field?
Any set which satisfies all eight axioms is called a complete ordered field. We assume the existence of a complete ordered field, called the real numbers. The real numbers are denoted by R.
Can the complex numbers be ordered?
TL;DR: The complex numbers are not an ordered field; there is no ordering of the complex numbers that is compatible with addition and multiplication. If a structure is a field and has an ordering, two additional axioms need to hold for it to be an ordered field.
What is the set of real numbers?
The real numbers include natural numbers or counting numbers, whole numbers, integers, rational numbers (fractions and repeating or terminating decimals), and irrational numbers. The set of real numbers is all the numbers that have a location on the number line.
#1 usability according to G2
Try the PDF solution that respects your time.