Compose Sum Application For Free
Drop document here to upload
Up to 100 MB for PDF and up to 25 MB for DOC, DOCX, RTF, PPT, PPTX, JPEG, PNG, JFIF, XLS, XLSX or TXT
Note: Integration described on this webpage may temporarily not be available.
0
Forms filled
0
Forms signed
0
Forms sent
Discover the simplicity of processing PDFs online

Upload your document in seconds

Fill out, edit, or eSign your PDF hassle-free

Download, export, or share your edited file instantly
Top-rated PDF software recognized for its ease of use, powerful features, and impeccable support






Every PDF tool you need to get documents done paper-free
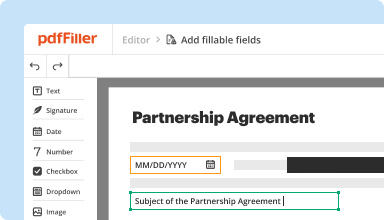
Create & edit PDFs
Generate new PDFs from scratch or transform existing documents into reusable templates. Type anywhere on a PDF, rewrite original PDF content, insert images or graphics, redact sensitive details, and highlight important information using an intuitive online editor.
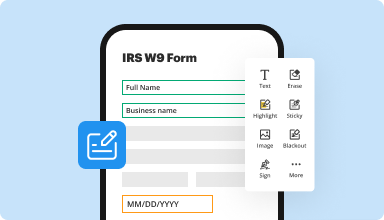
Fill out & sign PDF forms
Say goodbye to error-prone manual hassles. Complete any PDF document electronically – even while on the go. Pre-fill multiple PDFs simultaneously or extract responses from completed forms with ease.
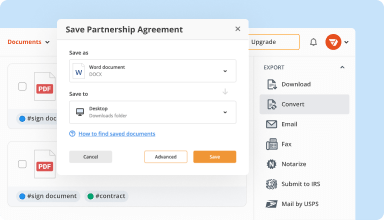
Organize & convert PDFs
Add, remove, or rearrange pages inside your PDFs in seconds. Create new documents by merging or splitting PDFs. Instantly convert edited files to various formats when you download or export them.
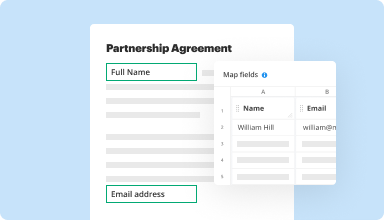
Collect data and approvals
Transform static documents into interactive fillable forms by dragging and dropping various types of fillable fields on your PDFs. Publish these forms on websites or share them via a direct link to capture data, collect signatures, and request payments.

Export documents with ease
Share, email, print, fax, or download edited documents in just a few clicks. Quickly export and import documents from popular cloud storage services like Google Drive, Box, and Dropbox.
Store documents safely
Store an unlimited number of documents and templates securely in the cloud and access them from any location or device. Add an extra level of protection to documents by locking them with a password, placing them in encrypted folders, or requesting user authentication.
Customer trust by the numbers
64M+
users worldwide
4.6/5
average user rating
4M
PDFs edited per month
9 min
average to create and edit a PDF
Join 64+ million people using paperless workflows to drive productivity and cut costs
Why choose our PDF solution?
Cloud-native PDF editor
Access powerful PDF tools, as well as your documents and templates, from anywhere. No installation needed.
Top-rated for ease of use
Create, edit, and fill out PDF documents faster with an intuitive UI that only takes minutes to master.
Industry-leading customer service
Enjoy peace of mind with an award-winning customer support team always within reach.
What our customers say about pdfFiller
See for yourself by reading reviews on the most popular resources:
I love being able to fill out forms that I wouldn't be able to normally. My handwriting can be hard to read and this makes it clean and clear. The others parties like it too! :)
2016-04-14
I have been using this program for almost 2 years now and it is amazing! I have uploaded all of my work documents/forms so I no longer have to hand write every single thing. Not to mention I am saving money by not having to purchase any paper and more importantly I don't have to purchase any printer ink.
2018-07-29
I really like the program; however, when I save I get logged out. I have not been successful at using any form except the Offer to Purchase. I need addendums.
2018-10-24
I own a few franchise restaurants and have to use this product about once a week and it makes my time with documents way faster and easier. I don't have to download a document, scan it, sign it, and then rescan it and then send it. I can do it all electronically thanks the PDFfiller.
2019-05-20
Interesting product the pdfFiller. I would like to learn what else I can do with this software. The new look for the PDF is wonderful but I don't know if I would be able to use the old PDF from Microsoft. It seems I just paid my Microsoft subscription. It seems that the PDF is a software of it's own and doesn't come with the Microsoft Tools.
2024-07-12
i app works well once you find the form you need. I'm having a problem creating new forms or updating existing ones with new information while saving the old ones.
2022-05-20
Professional look!
Got to know about PDFfiller because we use Salesforce at work, and these two are compatible. Taken together - tremendous time savings, at least several hours a week, i'd say!
Longer contracts might need a while to get fully visible on the screen, but no rush here
What do you think about this review?
2021-02-05
Easy to use with multi-functions
Very easy to use, several functions and formatting system. I have tried many PDF editors - this is the best of them all! Keep it up!
2020-10-21
Well , I'm learning
Well I'm still learning But the Draw option is AWESOME ,It lets you Sign in Real Time + It's Your Real Signature,Not a Generated one from putting text in a box and using thePC's script font to generate a signature .. Thanks Guys David Simmonsp.s.I'll let you know more as I learn to do more..Again Thanks..
2020-07-28
For pdfFiller’s FAQs
Below is a list of the most common customer questions. If you can’t find an answer to your question, please don’t hesitate to reach out to us.
What if I have more questions?
Contact Support
How do you create a Riemann sum?
0:37 6:16 Suggested clip Calculating a Definite Integral Using Riemann Sums — Part 1 YouTubeStart of suggested client of suggested clip Calculating a Definite Integral Using Riemann Sums — Part 1
What do I represent in Riemann sum?
A Riemann Sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. We saw that as we increased the number of intervals (and decreased the width of the rectangles) the sum of the areas of the rectangles approached the area under the curve.
What is the most accurate Riemann sum?
The midpoint Riemann sums is an attempt to balance these two extremes, so generally it is more accurate. The Mean Value Theorem for Integrals guarantees (for appropriate functions f) that a point c exists in [a, b] such that the area under the curve is equal to the area f(c)(BA).
How do you know if a Riemann sum is overestimate or underestimate?
If the graph is increasing on the interval, then the left-sum is an underestimate of the actual value and the right-sum is an overestimate. If the curve is decreasing then the right-sums are underestimates and the left-sums are overestimates.
Why do we use Riemann sums?
In mathematics, a Riemann sum is a certain kind of approximation of an integral by a finite sum. This approach can be used to find a numerical approximation for a definite integral even if the fundamental theorem of calculus does not make it easy to find a closed-form solution.
Why is the midpoint method more accurate?
The advantage of the midpoint method is that one obtains the same elasticity between two price points whether there is a price increase or decrease. This is because the formula uses the same base for both cases.
Video Review on How to Compose Sum Application
#1 usability according to G2
Try the PDF solution that respects your time.






