Inscribe Equation Transcript For Free
Drop document here to upload
Up to 100 MB for PDF and up to 25 MB for DOC, DOCX, RTF, PPT, PPTX, JPEG, PNG, JFIF, XLS, XLSX or TXT
Note: Integration described on this webpage may temporarily not be available.
0
Forms filled
0
Forms signed
0
Forms sent
Discover the simplicity of processing PDFs online

Upload your document in seconds

Fill out, edit, or eSign your PDF hassle-free

Download, export, or share your edited file instantly
Top-rated PDF software recognized for its ease of use, powerful features, and impeccable support






Every PDF tool you need to get documents done paper-free
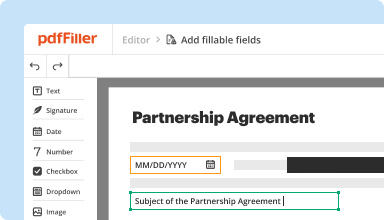
Create & edit PDFs
Generate new PDFs from scratch or transform existing documents into reusable templates. Type anywhere on a PDF, rewrite original PDF content, insert images or graphics, redact sensitive details, and highlight important information using an intuitive online editor.
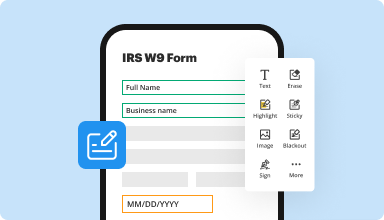
Fill out & sign PDF forms
Say goodbye to error-prone manual hassles. Complete any PDF document electronically – even while on the go. Pre-fill multiple PDFs simultaneously or extract responses from completed forms with ease.
Organize & convert PDFs
Add, remove, or rearrange pages inside your PDFs in seconds. Create new documents by merging or splitting PDFs. Instantly convert edited files to various formats when you download or export them.
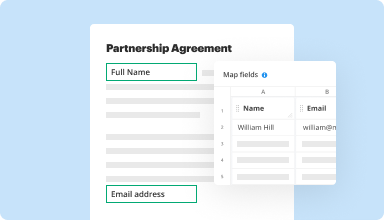
Collect data and approvals
Transform static documents into interactive fillable forms by dragging and dropping various types of fillable fields on your PDFs. Publish these forms on websites or share them via a direct link to capture data, collect signatures, and request payments.

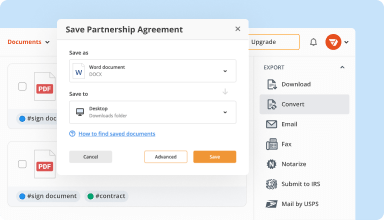
Export documents with ease
Share, email, print, fax, or download edited documents in just a few clicks. Quickly export and import documents from popular cloud storage services like Google Drive, Box, and Dropbox.
Store documents safely
Store an unlimited number of documents and templates securely in the cloud and access them from any location or device. Add an extra level of protection to documents by locking them with a password, placing them in encrypted folders, or requesting user authentication.
Customer trust by the numbers
64M+
users worldwide
4.6/5
average user rating
4M
PDFs edited per month
9 min
average to create and edit a PDF
Join 64+ million people using paperless workflows to drive productivity and cut costs
Why choose our PDF solution?
Cloud-native PDF editor
Access powerful PDF tools, as well as your documents and templates, from anywhere. No installation needed.
Top-rated for ease of use
Create, edit, and fill out PDF documents faster with an intuitive UI that only takes minutes to master.
Industry-leading customer service
Enjoy peace of mind with an award-winning customer support team always within reach.
What our customers say about pdfFiller
See for yourself by reading reviews on the most popular resources:
Easy to use, creates clean, professional looking documents, allows you to upload any form or document that needs to be filled out and fill it in as if you typed it, without needing the typewriter! Whether you scan a form, upload a text or spreadsheet document, even image files, you can fill in any information needed and customize fonts, size, color, highlight sections, even verified signatures and PDFfiller will align your input horizontally and vertically. You can even create templates of your forms. Easy to use intuitive interface. A definite value for the money.
2015-04-12
The program did not function as I anticipated, but after I played around with it, I realized it was still a useful tool. I am a Licensed Counselor and this is a great tool used to communicate and transmit sensitive information online. I highly recommend to others!
2018-01-15
For people who are not that good in technology like me (you are not to blame), it was a bit difficult to find a website where I could fill important documents to send via internet in a safe manner. After a while, I found your website and once I figured out how to save and send the documents I can say that it is a good website.
My recommendation is to make it even easier to access and follow directions for seasoned people like me.
Thanks
2018-05-03
the user interaction could be a little better, for example I don't like that when I'm on the Mybox tab, once I open a file and close it I keep getting directed to the dashboard. So I have to keep clicking back to the Mybox. Otherwise, great product! :)
2018-07-26
This is the most useful tool! When i first started using it, I had no idea how much I would later come to depend on PDF Filler! Thanks for making my home business a lot more productive. I've purchased a lot of tools to make things a lot easier but none have really delivered in the way PDFfiller has since it seems much of operating a small business (and life in general) is all about filling out form after form, lol.
2019-02-13
Valuable service four our business
Great for completing and revising forms
Allows easy efficient revisions to forms that are not otherwise "fill-in" online forms
website can be slow and clunky at times, technical support is only available through on-line chat, no teleconference service
2019-01-29
Katie's pdfFiller Review
My overall experience is wonderful!
The most impactful feature is being able to easily fill a PDF, download it, and send it to people.
I least like how hard it is to start a text box on a PDF.
2022-07-07
Thus far have managed to sign and complete forms, but can use a webinar to learn more. D id not know how to make changes that were not in the fillable portion.
2021-12-04
I just keep working towards being able…
I just keep working towards being able to afford this amazing tool. I am wondering if their is a discount when an Australian Charity or Not for Profit is utilising this Application.
2020-10-27
Inscribe Equation Transcript Feature
The Inscribe Equation Transcript feature offers a reliable solution for transforming complex math equations into clear, accessible text. This tool helps students, educators, and professionals manage mathematical expressions effortlessly.
Key Features
Converts handwritten math equations into text format
Supports a wide range of mathematical symbols and functions
Integrates seamlessly with educational and professional platforms
User-friendly interface that simplifies the input process
Offers real-time transcription for immediate feedback
Potential Use Cases and Benefits
Students can easily transcribe homework or exam notes for better organization
Educators may enhance lesson plans by converting written examples into digital format
Professionals can document mathematical models and analyses for presentations
Researchers can quickly digitize equations from collaborative discussions
Tutors can provide clearer explanations by displaying equations in text
Inscribe Equation Transcript can solve your problems by streamlining the way you handle mathematical equations. No more struggling with unclear notes or trying to remember complex formulas. This feature brings clarity and efficiency to your work, allowing you to focus on understanding and applying math effectively.
For pdfFiller’s FAQs
Below is a list of the most common customer questions. If you can’t find an answer to your question, please don’t hesitate to reach out to us.
What if I have more questions?
Contact Support
What is the formula of inscribed angle?
Inscribed Angle Theorem: The measure of an inscribed angle is half the measure of the intercepted arc. That is, Mac=12mAOC. This leads to the corollary that in a circle any two inscribed angles with the same intercepted arcs are congruent.
What is the definition of inscribed angle?
In geometry, an inscribed angle is the angle formed in the interior of a circle when two secant lines (or, in a degenerate case, when one secant line and one tangent line of that circle) intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.
How do you find the length of an arc with an inscribed angle?
Given the measure of an arc in degrees, the length of the arc can be found by multiplying the quotient of the given angle and 360 degrees to the length of the circumference of the circle.
How do you find the measure of an inscribed angle?
The measure of an inscribed angle is half the measure of the intercepted arc. That is, Mac=12mAOC. This leads to the corollary that in a circle any two inscribed angles with the same intercepted arcs are congruent.
Which is an inscribed angle?
An inscribed angle is an angle formed by two chords in a circle which have a common endpoint. This common endpoint forms the vertex of the inscribed angle. The other two endpoints define what we call an intercepted arc on the circle. ... It says that the measure of the intercepted arc is twice that of the inscribed angle.
Why are inscribed angles half the arc?
The inscribed angle theorem states that an angle inscribed in a circle is half of the central angle 2 that subtends the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the circle.
How do I find the length of an arc?
To find arc length, start by dividing the arc's central angle in degrees by 360. Then, multiply that number by the radius of the circle. Finally, multiply that number by 2 × pi to find the arc length.
Is a central angle and inscribed angle?
A central angle is an angle formed by two radii with the vertex at the center of the circle. In the diagram at the right, AOB is a central angle with an intercepted minor arc from A to B. ... An inscribed angle is an angle with its vertex “on” the circle, formed by two intersecting chords.
What's the relationship between a central angle and its corresponding arc?
A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B. Central angles are subtended by an arc between those two points, and the arc length is the central angle of a circle of radius one (measured in radians).
What is the central angle theorem?
Theorem: Central Angle Theorem The Central Angle Theorem states that the central angle from two chosen points A and B on the circle is always twice the inscribed angle from those two points. The inscribed angle can be defined by any point along the outer arc AB and the two points A and B.
#1 usability according to G2
Try the PDF solution that respects your time.






