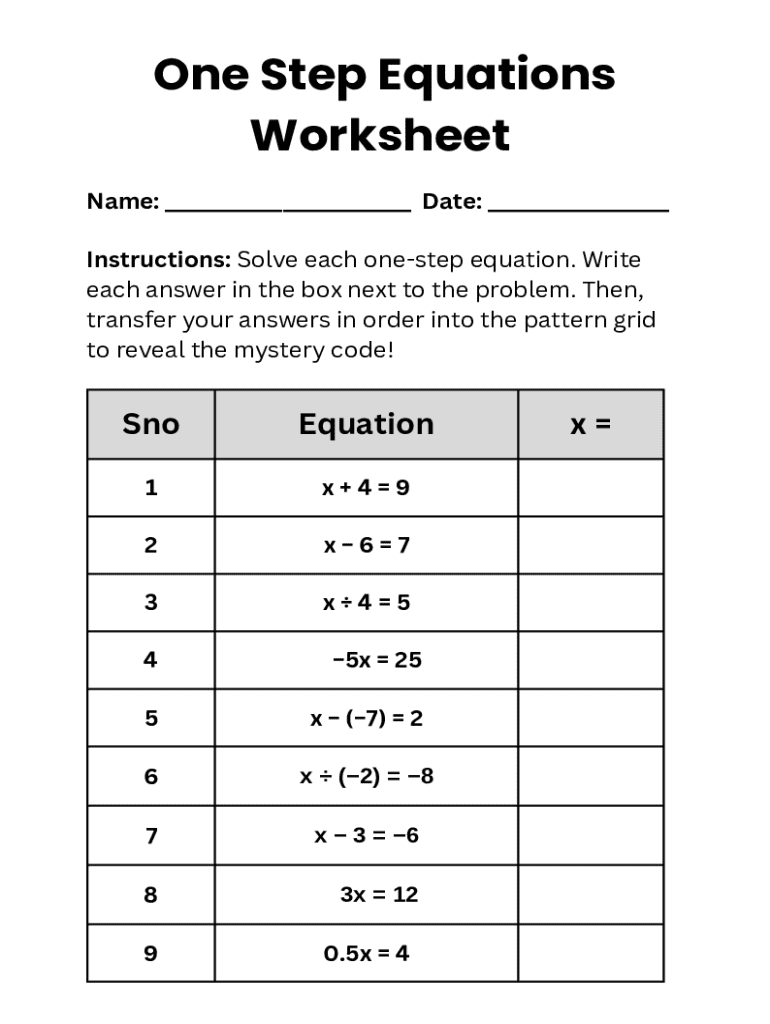
Get the free One Step Equations

This worksheet is designed for students to practice solving one-step equations and revealing a mystery code through their answers.

How to fill out one step equations

How to fill out one step equations

1. Identify the equation you need to solve.
2. Isolate the variable on one side of the equation.
3. Determine the operation that is currently applied to the variable (addition, subtraction, multiplication, or division).
4. Apply the inverse operation to both sides of the equation to eliminate the operation.
5. Simplify both sides if necessary.
6. Check your solution by substituting the value back into the original equation.

Who needs one step equations?

1. Students learning algebra.
2. Individuals preparing for standardized tests.
3. Anyone needing to solve basic math problems in everyday life.
4. Professionals in fields that require mathematical calculations.

One step equations form: A comprehensive how-to guide

Understanding one-step equations

One-step equations are mathematical statements that equate two expressions and require only a single operation to isolate the variable. Typically represented in the form of x + a = b or x - a = b, these equations form the bedrock of algebraic understanding. Grasping the fundamentals of one-step equations is crucial for progressing in algebra and beyond.

The significance of one-step equations lies in their simplicity, making them an excellent starting point for learners new to algebra. They provide a clear framework for understanding how to manipulate variables and can be extended to more complex equations. Practical applications range from budgeting scenarios to calculating distances, demonstrating their relevance in everyday life.

• One-step equations enable individuals to develop critical thinking and problem-solving skills.
• Many careers utilize algebraic principles, highlighting the value of mastering one-step equations.

Types of one-step equations

One-step equations can be categorized based on the type of operation involved: addition, subtraction, multiplication, and division. Each type has distinct characteristics and requires unique strategies for solving.

Addition and subtraction equations

In addition equations, such as x + 5 = 12, the goal is to isolate the variable by performing the opposite operation—subtraction in this case. To solve this, you subtract 5 from both sides, leading to x = 7. Common mistakes include failing to perform operations on both sides or misreading the equation.

Multiplication and division equations

With multiplication equations like 3x = 12, dividing both sides by 3 allows for the isolation of x. Hence, x = 4. Providing visual aids like balance scales can enhance understanding, reinforcing the idea of maintaining balance in equations.

Equations involving negatives

Managing equations with negative values requires careful interpretation, as in the case of x - 4 = -2. Adding 4 to both sides yields x = 2. Always remember that incorrect handling of negative signs is a prevalent issue among learners. Practicing with practical examples can help to mitigate this challenge.

Step-by-step guide on solving one-step equations

To effectively solve one-step equations, it’s essential to follow a systematic approach.

• Identify whether addition, subtraction, multiplication, or division is needed based on the equation setup.
• Use inverse operations to isolate the variable efficiently.
• Always substitute your solution back into the original equation to verify its accuracy.

For instance, in solving the equation x + 3 = 10, you would isolate x by subtracting 3 from both sides, yielding x = 7. This ensures clarity in the problem-solving process and fosters a comprehensive understanding of the equations at hand.

Interactive tools for practice

Leveraging interactive tools can significantly enhance one’s grasp of one-step equations. There are a variety of online resources and tools available to practice and solidify your understanding.

Online worksheets and tools

Websites offering worksheets specifically designed for one-step equations allow users to customize their learning experience. Interactive quizzes can make practice sessions engaging and productive.

Engaging with Google forms quizzes

Creating assessments with Google Forms is an effective way to self-evaluate comprehension. Users can generate quizzes that address various difficulties, providing instant feedback for improvement.

Printable worksheets

Printable worksheets serve as an excellent tool for offline practice. Creating your templates with services like pdfFiller can streamline the process, ensuring that you have the right resources at your fingertips.

Common challenges and how to overcome them

Learners often face hurdles when working with one-step equations. However, identifying these challenges can lead to effective strategies for overcoming them.

• Ensure that you correctly interpret the equations before solving. Practice formulation to develop better intuition.
• Double-check calculations and consider writing out steps to avoid errors.
• Maintain awareness of signs; practicing with a focus on accuracy can mitigate this issue.

By consistently working on these common pitfalls, learners can improve their proficiency in solving one-step equations and gain confidence.

Practice problems with solutions

Regular practice is paramount for mastering one-step equations. Here are several practice problems segmented by difficulty levels.

Basic practice problems

For beginners, consider starting with simple problems such as: x + 2 = 5, x - 3 = 1. Solutions are straightforward: for the first, x = 3; for the second, x = 4.

Intermediate problems

Intermediate challenges might include 2x = 10 and x - 7 = -2, with solutions of x = 5 and x = 5, respectively. These problems require a slightly deeper understanding and manipulation of the equations.

Advanced problem sets

For those seeking to master one-step equations, consider tackling more complex problems like 5 - x = 3 or -3x = -9. The solutions are x = 2 and x = 3. Mastery of these problems solidifies your algebraic abilities.

Utilizing pdfFiller for document creation and management

Empowering your learning process with pdfFiller can streamline your experience with one-step equations. The platform provides a wealth of features that enhance document management related to educational resources.

Features overview

With pdfFiller, users can edit PDFs, sign electronic documents, and collaborate seamlessly. Features such as annotation tools allow for easy adjustments to worksheets and practice sheets, ensuring an optimal learning environment.

Step-by-step instructions to use pdfFiller

Creating and managing equation worksheets is simple with pdfFiller. Begin by uploading a document, utilize editing tools to annotate problems, and easily share your work with peers for collaboration or feedback.

Benefits of cloud-based document management

One of the standout advantages of pdfFiller is its cloud-based nature. Users can access documents from anywhere, enabling flexibility in study locations. Additionally, collaboration on documents can enrich learning outcomes and foster teamwork.

Engaging learning methods

Implementing varied learning methods can keep students engaged and enhance their grasp of one-step equations.

Incorporating games into learning

Educational games targeting one-step equations can make learning enjoyable. Games like 'Equation Bingo' or digital platforms that utilize gamified assessments create a stimulating environment for practice.

Visual learning aids

Utilizing visual aids like charts or graphs can help students comprehend concepts more intuitively. Visualizing equations as balanced scales or number lines can illustrate the importance of equality in equations.

Collaborative learning techniques

Engaging in group activities allows peers to explain concepts to one another, fostering deeper understanding. Peer mentoring techniques can provide diverse insights into solving one-step equations.

Additional tips and strategies

Efficient study strategies are essential for mastering one-step equations. Here are several additional tips to further your learning.

• Creating a structured time-table can ensure consistent practice and retention of concepts.
• Consider exploring various online courses, workshops, or textbooks that focus on algebra fundamentals.
• Set personal goals and track progress to maintain motivation throughout your algebra journey.

For pdfFiller’s FAQs

How do I modify my one step equations in Gmail?

Using pdfFiller's Gmail add-on, you can edit, fill out, and sign your one step equations and other papers directly in your email. You may get it through Google Workspace Marketplace. Make better use of your time by handling your papers and eSignatures.

How do I edit one step equations online?

The editing procedure is simple with pdfFiller. Open your one step equations in the editor. You may also add photos, draw arrows and lines, insert sticky notes and text boxes, and more.

How do I edit one step equations on an iOS device?

Yes, you can. With the pdfFiller mobile app, you can instantly edit, share, and sign one step equations on your iOS device. Get it at the Apple Store and install it in seconds. The application is free, but you will have to create an account to purchase a subscription or activate a free trial.

What is one step equations?

One step equations are algebraic equations that can be solved in a single operation, involving addition, subtraction, multiplication, or division.

Who is required to file one step equations?

Individuals who need to report their income or other financial information in a simplified manner may be required to file one step equations, typically in a basic context.

How to fill out one step equations?

To fill out one step equations, isolate the variable on one side of the equation by performing the same operation on both sides.

What is the purpose of one step equations?

The purpose of one step equations is to simplify the process of solving for unknown variables in mathematical problems.

What information must be reported on one step equations?

Information that must be reported includes the variable being solved for and the constants involved in the equation.